Skip to main content

Section 9.3 Uncountable Sets

Beginning Activity The Game of Dodge Ball
A4US

(From The Heart of Mathematics: An Invitation to Effective Thinking by Edward B. Burger and Michael Starbird, Key Publishing Company, © 2000 by Edward B. Burger and Michael Starbird.)

Dodge Ball is a game for two players. It is played on a game board such as the one shown in Figure 9.24 and Figure 9.25.

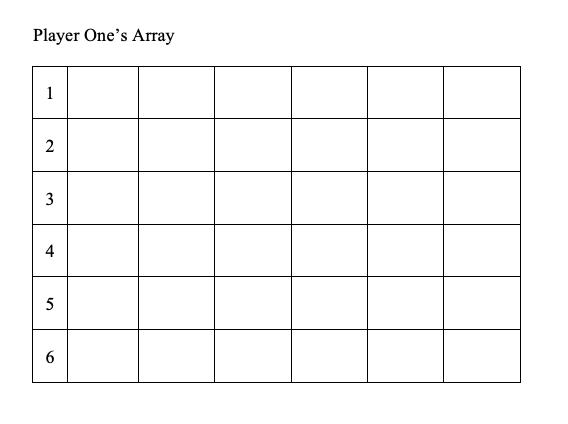
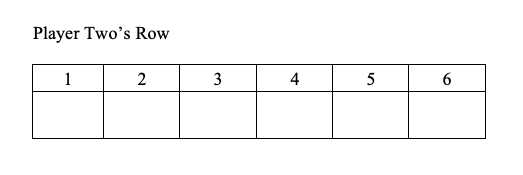
Figure 9.24. Game Board for Dodge Ball: Player 1
Figure 9.25. Game Board for Dodge Ball: Player 2

Player One has a 6 by 6 array to complete and Player Two has a 1 by 6 row to complete. Each player has six turns as described next.

  • Player One begins by filling in the first horizontal row of his or her table with a sequence of six X's and O's, one in each square in the first row.

  • Then Player Two places either an X or an O in the first box of his or her row. At this point, Player One has completed the first row and Player Two has filled in the first box of his or her row with one letter.

  • The game continues with Player One completing a row with six letters (X's and O's), one in each box of the next row followed by Player Two writing one letter (an X or an O) in the next box of his or her row. The game is completed when Player One has completed all six rows and Player Two has completed all six boxes in his or her row.

  • Player One wins if any horizontal row in the 6 by 6 array is identical to the row that Player Two created. (Player One matches Player Two.)

  • Player Two wins if Player Two's row of six letters is different than each of the six rows produced by Player One. (Player Two “dodges” Player One.)

There is a winning strategy for one of the two players. This means that there is plan by which one of the two players will always win. Which player has a winning strategy? Carefully describe this winning strategy.

Applying the Winning Strategy to Lists of Real Numbers.

Following is a list of real numbers between 0 and 1. Each real number is written as a decimal number.

\begin{align*} a_1 \amp = 0.1234567890 \amp a_6 \amp = 0.0103492222\\ a_2 \amp = 0.3216400000 \amp a_7 \amp = 0.0011223344\\ a_3 \amp = 0.4321593333 \amp a_8 \amp = 0.7077700022\\ a_4 \amp = 0.9120930092 \amp a_9 \amp = 0.2100000000\\ a_5 \amp = 0.0000234102 \amp a_{10} \amp = 0.9870008943 \end{align*}

Use a method similar to the winning strategy in the game of Dodge Ball to write a real number (in decimal form) between 0 and 1 that is not in this list of 10 numbers.

1.

Do you think your method could be used for any list of 10 real numbers between 0 and 1 if the goal is to write a real number between 0 and 1 that is not in the list?

2.

Do you think this method could be extended to a list of 20 different real numbers? To a list of 50 different real numbers?

3.

Do you think this method could be extended to a countably infinite list of real numbers?

Beginning Activity Beginning Activity 2: Functions from a Set to Its Power Set
A4US

Let \(A\) be a set. In Section 5.1, we defined the power set \(\mathcal{P} ( A )\) of \(A\) to be the set of all subsets of \(A\text{.}\) This means that \(X \in \mathcal{P} ( A )\) if and only if \(X \subseteq A\text{.}\) Theorem 5.9 in Section 5.1 states that if a set \(A\) has \(n\) elements, then \(A\) has \(2^n\) subsets or that \(\mathcal{P} ( A )\) has \(2^n\) elements. Using our current notation for cardinality, this means that if \(\text{ card} ( A ) = n\text{,}\) then \(\text{ card} ( \mathcal{P} ( A ) ) = 2^n\text{.}\) (The proof of this theorem was Activity 29.)

We are now going to define and explore some functions from a set \(A\) to its power set \(\mathcal{P} ( A )\text{.}\) This means that the input of the function will be an element of \(A\) and the output of the function will be a subset of \(A\text{.}\)

1.

Let \(A = \left\{1, 2, 3, 4 \right\}\text{.}\) Define \(f\x A \to \mathcal{P} ( A )\) by

\begin{align*} f ( 1 ) \amp = \left\{ 1, 2, 3 \right\} \amp f ( 2 ) \amp = \left\{ 1, 3, 4 \right\}\\ f ( 3 ) \amp = \left\{ 1, 4 \right\} \amp f ( 4 ) \amp = \left\{ 2, 4 \right\} \end{align*}
(a)

Is \(1 \in f ( 1 )\text{?}\) Is \(2 \in f ( 2 )\text{?}\) Is \(3 \in f ( 3 )\text{?}\) Is \(4 \in f ( 4 )\text{?}\)

(b)

Determine \(S = \left\{ x \in A \mid x \notin f ( x ) \right\}\text{.}\)

(c)

Notice that \(S \in \mathcal{P} ( A )\text{.}\) Does there exist an element \(t\) in \(A\) such that \(f ( t ) = S\text{?}\) That is, is \(S \in \text{ range} ( f )\text{?}\)

2.

Let \(A = \left\{1, 2, 3, 4 \right\}\text{.}\) Define \(f\x A \to \mathcal{P} ( A )\) by

\begin{equation*} f ( x ) = A - \left\{ x \right\} \text{ for each } x \in A\text{.} \end{equation*}
(a)

Determine \(f ( 1 )\text{.}\) Is \(1 \in f ( 1 )\text{?}\)

(b)

Determine \(f ( 2 )\text{.}\) Is \(2 \in f ( 2 )\text{?}\)

(c)

Determine \(f ( 3 )\text{.}\) Is \(3 \in f ( 3 )\text{?}\)

(d)

Determine \(f ( 4 )\text{.}\) Is \(4 \in f ( 4 )\text{?}\)

(e)

Determine \(S = \left\{ x \in A \mid x \notin f ( x ) \right\}\text{.}\)

(f)

Notice that \(S \in \mathcal{P} ( A )\text{.}\) Does there exist an element \(t\) in \(A\) such that \(f ( t ) = S\text{?}\) That is, is \(S \in \text{ range} ( f )\text{?}\)

3.

Define \(f\x \mathbb{N} \to \mathcal{P} ( \mathbb{N} )\) by

\begin{equation*} f ( n ) = \mathbb{N} - \left\{n^2, n^2-2n \right\}, \text{ for each } n \in \mathbb{N}\text{.} \end{equation*}
(a)

Determine \(f ( 1 )\text{,}\) \(f ( 2 )\text{,}\) \(f ( 3 )\text{,}\) and \(f ( 4 )\text{.}\) In each of these cases, determine if \(k \in f ( k )\text{.}\)

(b)

Prove that if \(n > 3\text{,}\) then \(n \in f ( n )\text{.}\)

Hint.

Prove that if \(n >3\text{,}\) then \(n^2 > n\) and \(n^2 - 2n >n\text{.}\)

(c)

Determine \(S = \left\{ x \in \mathbb{N} \mid x \notin f ( x ) \right\}\text{.}\)

(d)

Notice that \(S \in \mathcal{P} ( \mathbb{N} )\text{.}\) Does there exist an element \(t\) in \(\mathbb{N}\) such that \(f ( t ) = S\text{?}\) That is, is \(S \in \text{ range} ( f )\text{?}\)

We have seen examples of sets that are countably infinite, but we have not yet seen an example of an infinite set that is uncountable. We will do so in this section. The first example of an uncountable set will be the open interval of real numbers \(( 0, 1 )\text{.}\) The proof that this interval is uncountable uses a method similar to the winning strategy for Player Two in the game of Dodge Ball from Beginning Activity 1. Before considering the proof, we need to state an important result about decimal expressions for real numbers.

Subsection Decimal Expressions for Real Numbers

In its decimal form, any real number \(a\) in the interval \(( 0, 1 )\) can be written as \(a = 0.a_1 a_2 a_3 a_4 \ldots \text{,}\) where each \(a_i\) is an integer with \(0 \leq a_i \leq 9\text{.}\) For example,

\begin{equation*} \frac{5}{12} = 0.416666 \ldots\text{.} \end{equation*}

We often abbreviate this as \(\dfrac{5}{12} = 0.41 \overline{6}\) to indicate that the \(6\) is repeated. We can also repeat a block of digits. For example, \(\dfrac{5}{26} = 0.19 \overline{230769}\) to indicate that the block 230769 repeats. That is,

\begin{equation*} \frac{5}{26} = 0.19230769230769230769 \ldots\text{.} \end{equation*}

There is only one situation in which a real number can be represented as a decimal in more than one way. A decimal that ends with an infinite string of 9's is equal to one that ends with an infinite string of 0's. For example, \(0.3199999 \ldots\) represents the same real number as \(0.3200000 \ldots \text{.}\) Geometric series can be used to prove that a decimal that ends with an infinite string of 9's is equal to one that ends with an infinite string of 0's, but we will not do so here.

Definition.

A decimal representation of a real number \(a\) is in normalized form provided that there is no natural number \(k\) such that for all natural numbers \(n\) with \(n > k\text{,}\) \(a_n = 9\text{.}\) That is, the decimal representation of \(a\) is in normalized form if and only if it does not end with an infinite string of 9's.

One reason the normalized form is important is the following theorem (which will not be proved here).

Subsection Uncountable Subsets of \(\boldsymbol{\mathbb{R}}\)

In the proof that follows, we will use only the normalized form for the decimal representation of a real number in the interval \(( 0, 1 )\text{.}\)

Proof.

Since the interval \(( 0, 1 )\) contains the infinite subset \(\left\{\dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \ldots \,\right\}\text{,}\) we can use Theorem 9.11, to conclude that \(( 0, 1 )\) is an infinite set. So \(( 0, 1 )\) is either countably infinite or uncountable. We will prove that \(( 0, 1 )\) is uncountable by proving that any function from \(\N\) to \((0, 1)\) is not a surjection, and hence, there is no bijection from \(\N\) to \((0, 1)\text{.}\)

So suppose that \(f\x \mathbb{N} \to ( 0, 1 )\) is a function. We will show that \(f\) is not a surjection by showing that there exists an element in \(( 0, 1 )\) that cannot be in the range of \(f\text{.}\) Writing the images of the elements of \(\mathbb{N}\) in normalized form, we can write

\begin{align*} f ( 1 ) \amp = 0.a_{1 1} a_{1 2} a_{1 3} a_{1 4} a_{1 5} \ldots\\ f ( 2 ) \amp = 0.a_{2 1} a_{2 2} a_{2 3} a_{2 4} a_{2 5} \ldots\\ f ( 3 ) \amp = 0.a_{3 1} a_{3 2} a_{3 3} a_{3 4} a_{3 5} \ldots\\ f ( 4 ) \amp = 0.a_{4 1} a_{4 2} a_{4 3} a_{4 4} a_{4 5} \ldots\\ f ( 5 ) \amp = 0.a_{5 1} a_{5 2} a_{5 3} a_{5 4} a_{5 5} \ldots\\ \amp \vdots\\ f ( n ) \amp = 0.a_{n 1} a_{n 2} a_{n 3} a_{n 4} a_{n 5} \ldots\\ \amp \vdots \end{align*}

Notice the use of the double subscripts. The number \(a_{i j}\) is the \(j^\text{ th }\) digit to the right of the decimal point in the normalized decimal representation of \(f ( i )\text{.}\)

We will now construct a real number \(b = 0.b_1 b_2 b_3 b_4 b_5 \ldots\) in \(( 0, 1 )\) and in normalized form that is not in this list.

Note: The idea is to start in the upper left corner and move down the diagonal in a manner similar to the winning strategy for Player Two in the game in Beginning Activity 1. At each step, we choose a digit that is not equal to the diagonal digit.

Start with \(a_{1 1}\) in \(f ( 1 )\text{.}\) We want to choose \(b_1\) so that \(b_1 \ne 0\text{,}\) \(b_1 \ne a_{1 1}\text{,}\) and \(b_1 \ne 9\text{.}\) (To ensure that we end up with a decimal that is in normalized form, we make sure that each digit is not equal to 9.) We then repeat this process with \(a_{2 2}\text{,}\) \(a_{3 3}\text{,}\) \(a_{4 4}\text{,}\) \(a_{5 5}\text{,}\) and so on. So we let \(b\) be the real number \(b = 0.b_1 b_2 b_3 b_4 b_5 \ldots \text{,}\) where for each \(k \in \mathbb{N}\)

\begin{equation*} b_k = \begin{cases}3 \amp \text{if \(a_{k k} \ne 3\)} \\ 5 \amp \text{if \(a_{k k} = 3\).} \end{cases} \end{equation*}

(The choice of 3 and 5 is arbitrary. Other choices of distinct digits will also work.)

Now for each \(n \in \mathbb{N}\text{,}\) \(b \ne f ( n )\) since \(b\) and \(f ( n )\) are in normalized form and \(b\) and \(f ( n )\) differ in the \(n\){th} decimal place. Therefore, \(f\) is not a surjection. This proves that any function from \(\mathbb{N}\) to \(( 0, 1 )\) is not a surjection and hence, there is no bijection from \(\mathbb{N}\) to \(( 0, 1 )\text{.}\) Therefore, \(( 0, 1 )\) is not countably infinite and hence must be an uncountable set.

Progress Check 9.28. Dodge Ball and Cantor's Diagonal Argument.

The proof of Theorem 9.27 is often referred to as Cantor's diagonal argument. It is named after the mathematician Georg Cantor, who first published the proof in 1874. Explain the connection between the winning strategy for Player Two in Dodge Ball (see Beginning Activity 1) and the proof of Theorem 9.27 using Cantor's diagonal argument.

Solution.

Player Two has a winning strategy. On the \(k\)th turn, whatever symbol Player One puts in the \(k\)th position of the \(k\)th row, Player Two must put the other symbol in the \(k\)th position of his or her row. This guarantees that the row of symbols produced by Player Two will be different than any of the rows produced by Player One.

This is the same idea used in Cantor's Diagonal Argument. Once we have a “list” of real numbers in normalized form, we create a real number that is not in the list by making sure that its \(k\)th decimal place is different than the \(k\)th decimal place for the \(k\)th number in the list. The one complication is that we must make sure that our new real number does not have a decimal expression that ends in all 9's. This was done by using only 3's and 5's.

The open interval \(( 0, 1 )\) is our first example of an uncountable set. The cardinal number of \(( 0, 1 )\) is defined to be \(\boldsymbol{c}\text{,}\) which stands for the cardinal number of the continuum. So the two infinite cardinal numbers we have seen are \(\aleph_0\) for countably infinite sets and \(\boldsymbol{c}\text{.}\)

Definition.

A set \(A\) is said to have cardinality \(\boldsymbol{c}\) provided that \(A\) is equivalent to \(( 0, 1 )\text{.}\) In this case, we write \(\text{ card} ( A ) = \boldsymbol{c}\) and say that the cardinal number of \(A\) is \(\boldsymbol{c}\text{.}\)

The proof of Theorem 9.29 is included in Progress Check 9.30.

Progress Check 9.30. Proof of Theorem 9.29.

(a)

In Task 9.2.c of Progress Check 9.2, we proved that if \(b \in \R\) and \(b > 0\text{,}\) then the open interval \(( 0, 1 )\) is equivalent to the open interval \(( 0, b )\text{.}\) Now let \(a\) and \(b\) be real numbers with \(a \lt b\text{.}\) Find a function

\begin{equation*} f\x ( 0, 1 ) \to ( a, b ) \end{equation*}

that is a bijection and conclude that the open interval \(( 0, 1) \approx ( a, b )\text{.}\)

Hint.

Find a linear function that passes through the points \(( 0, a )\) and \(( 1, b )\text{.}\) Use this to define the function \(f\text{.}\) Make sure you prove that this function \(f\) is a bijection.

Solution.
Proof.

In order to find a bijection \(f\x ( 0, 1 ) \to ( a, b )\text{,}\) we will use the linear function through the points \(( 0, a )\) and \(( 1, b )\text{.}\) The slope is \(( b - a)\) and the \(y\)-intercept is \(( 0, a )\text{.}\) So define \(f\x ( 0, 1 ) \to ( a, b )\) by \(f ( x ) = ( b - a )x + a\text{,}\) for each \(x \in ( 0, 1 )\text{.}\) Now, if \(x, t \in ( 0, 1 )\) and \(f ( x ) = f ( t )\text{,}\) then

\begin{equation*} ( b - a )x + a = ( b - a )t + a\text{.} \end{equation*}

This implies that \(( b - a )x = ( b - a )t\text{,}\) and since \(b - a \ne 0\text{,}\) we can conclude that \(x = t\text{.}\) Therefore, \(f\) is an injection.

To prove that \(f\) is a surjection, we let \(y \in ( a, b )\text{.}\) If \(x = \dfrac{y - a}{b - a}\text{,}\) then

\begin{align*} f ( x ) \amp = f \!\left( \frac{y - a}{b - a} \right)\\ \amp = ( b - a ) \!\left( \frac{y - a}{b - a} \right) + a\\ \amp = ( y - a ) + a\\ \amp = y\text{.} \end{align*}

This proves that \(f\) is a surjection. Hence, \(f\) is a bijection and \(( 0, 1 ) \approx ( a, b )\text{.}\) Therefore, \(( a, b )\) is uncountable and has cardinality \(\boldsymbol{c}\text{.}\)

(b)

Let \(a, b, c, d\) be real numbers with \(a \lt b\) and \(c \lt d\text{.}\) Prove that the open interaval \(( a, b )\) is equivalent to the open interval \(( c, d )\text{.}\)

Solution.

Now, if \(a, b, c, d\) are real numbers with \(a \lt b\) and \(c \lt d\text{,}\) then we know that \(( a, b ) \approx ( 0, 1 )\) and \(( c, d ) \approx ( 0, 1 )\text{.}\) Since \(\approx\) is an equivalence relation,we can conclude that \(( a, b ) \approx ( c, d )\text{.}\)

Proof.

Let \(f\x \left( -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right) \to \mathbb{R}\) be defined by \(f ( x ) = \tan x\text{,}\) for each \(x \in \mathbb{R}\text{.}\) The function \(f\) is a bijection and, hence, \(\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2} \right) \approx \mathbb{R}\text{.}\) So by Theorem 9.29, \(\mathbb{R}\) is uncountable and has cardinality \(\boldsymbol{c}\text{.}\)

Subsection Cantor's Theorem

We have now seen two different infinite cardinal numbers, \(\aleph_0\) and \(\boldsymbol{c}\text{.}\) It can seem surprising that there is more than one infinite cardinal number. A reasonable question at this point is, “Are there any other infinite cardinal numbers?” The astonishing answer is that there are, and in fact, there are infinitely many different infinite cardinal numbers. The basis for this fact is the following theorem, which states that a set is not equivalent to its power set. The proof is due to Georg Cantor (1845–1918), and the idea for this proof was explored in Beginning Activity 2. The basic idea of the proof is to prove that any function from a set \(A\) to its power set cannot be a surjection.

Proof.

Let \(A\) be a set. If \(A = \emptyset\text{,}\) then \(\mathcal{P} ( A ) = \left\{ \emptyset \right\}\text{,}\) which has cardinality 1. Therefore, \(\emptyset\) and \(\mathcal{P} ( \emptyset )\) do not have the same cardinality.

Now suppose that \(A \ne \emptyset\text{,}\) and let \(f\x A \to \mathcal{P} ( A )\text{.}\) We will show that \(f\) cannot be a surjection, and hence there is no bijection from \(A\) to \(\mathcal{P} ( A )\text{.}\) This will prove that \(A\) is not equivalent to \(\mathcal{P} ( A )\text{.}\) Define

\begin{equation*} S = \left\{ x \in A \mid x \notin f ( x ) \right\}\text{.} \end{equation*}

Assume that there exists a \(t\) in \(A\) such that \(f ( t ) = S\text{.}\) Now, either \(t \in S\) or \(t \notin S\text{.}\)

  • If \(t \in S\text{,}\) then \(t \in \left\{ x \in A \mid x \notin f ( x ) \right\}\text{.}\) By the definition of \(S\text{,}\) this means that \(t \notin f ( t )\text{.}\) However, \(f ( t ) = S\) and so we conclude that \(t \notin S\text{.}\) But now we have \(t \in S\) and \(t \notin S\text{.}\) This is a contradiction.

  • If \(t \notin S\text{,}\) then \(t \notin \left\{ x \in A \mid x \notin f ( x ) \right\}\text{.}\) By the definition of \(S\text{,}\) this means that \(t \in f ( t )\text{.}\) However, \(f ( t ) = S\) and so we conclude that \(t \in S\text{.}\) But now we have \(t \notin S\) and \(t \in S\text{.}\) This is a contradiction.

So in both cases we have arrived at a contradiction. This means that there does not exist a \(t\) in \(A\) such that \(f ( t ) = S\text{.}\) Therefore, any function from \(A\) to \(\mathcal{P} ( A )\) is not a surjection and hence not a bijection. Hence, \(A\) and \(\mathcal{P} ( A )\) do not have the same cardinality.

Proof.

Since \(\mathcal{P} ( \mathbb{N} )\) contains the infinite subset \(\left\{ \left\{ 1 \right\}, \left\{ 2 \right\}, \left\{ 3 \right\} \ldots \,\right\}\text{,}\) we can use Theorem 9.11, to conclude that \(\mathcal{P} ( \mathbb{N} )\) is an infinite set. By Cantor's Theorem (Theorem 9.32), \(\mathbb{N}\) and \(\mathcal{P} ( \mathbb{N} )\) do not have the same cardinality. Therefore, \(\mathcal{P} ( \mathbb{N} )\) is not countable and hence is an uncountable set.

Subsection Some Final Comments about Uncountable Sets

  1. We have now seen that any open interval of real numbers is uncountable and has cardinality \(\boldsymbol{c}\text{.}\) In addition, \(\mathbb{R}\) is uncountable and has cardinality \(\boldsymbol{c}\text{.}\) Now, Corollary 9.33 tells us that \(\mathcal{P} ( \mathbb{N} )\) is uncountable. A question that can be asked is, “Does \(\mathcal{P} ( \mathbb{N} )\) have the same cardinality as \(\mathbb{R}\text{?}\)” The answer is yes, although we are not in a position to prove it yet. A proof of this fact uses the following theorem, which is known as the Cantor-Schröder-Bernstein Theorem.

    In the statement of this theorem, notice that it is not required that the function \(g\) be the inverse of the function \(f\text{.}\) We will not prove the Cantor-Schröder-Bernstein Theorem here. The following items will show some uses of this important theorem.

  2. The Cantor-Schröder-Bernstein Theorem can also be used to prove that the closed interval \([ 0, 1 ]\) is equivalent to the open interval \(( 0, 1 )\text{.}\) See Exercise 6.

  3. Another question that was posed earlier is, “Are there other infinite cardinal numbers other than \(\aleph_0\) and \(\boldsymbol{c}\text{?}\)” Again, the answer is yes, and the basis for this is Cantor's Theorem (Theorem 9.32). We can start with \(\text{ card} ( \mathbb{N} ) = \aleph_0\text{.}\) We then define the following infinite cardinal numbers:

    \begin{align*} \amp \text{ card} ( \mathcal{P} ( \mathbb{N} ) ) = \alpha_1 \amp \amp \text{ card} ( \mathcal{P} ( \mathcal{P} ( \mathbb{N} ) ) ) = \alpha_2\\ \amp \text{ card} ( \mathcal{P} ( \mathcal{P} ( \mathcal{P} ( \mathbb{N} ) ) ) ) = \alpha_3 \amp \amp \vdots \end{align*}

    Cantor's Theorem tells us that these are all different cardinal numbers, and so we are just using the lowercase Greek letter \(\alpha\) (alpha) to help give names to these cardinal numbers. In fact, although we will not define it here, there is a way to “order” these cardinal numbers in such a way that

    \begin{equation*} \aleph_0 \lt \alpha_1 \lt \alpha_2 \lt \alpha_3 \lt \cdots\text{.} \end{equation*}

    Keep in mind, however, that even though these are different cardinal numbers, Cantor's Theorem does not tell us that these are the only cardinal numbers.

  4. In Comment 1, we indicated that \(\mathcal{P} ( \mathbb{N} )\) and \(\mathbb{R}\) have the same cardinality. Combining this with the notation in Comment 3, this means that

    \begin{equation*} \alpha_1 = \boldsymbol{c}\text{.} \end{equation*}

    However, this does not necessarily mean that \(\boldsymbol{c}\) is the “next largest” cardinal number after \(\aleph_0\text{.}\) A reasonable question is, “Is there an infinite set with cardinality between \(\aleph_0\) and \(\boldsymbol{c}\text{?}\)” Rewording this in terms of the real number line, the question is, “On the real number line, is there an infinite set of points that is not equivalent to the entire line and also not equivalent to the set of natural numbers?” This question was asked by Cantor, but he was unable to find any such set. He conjectured that no such set exists. That is, he conjectured that \(\boldsymbol{c}\) is really the next cardinal number after \(\aleph_0\text{.}\) This conjecture has come to be known as the Continuum Hypothesis. Stated somewhat more formally, the Continuum Hypothesis is

    There is no set \(X\) such that \(\aleph_0 \lt \text{ card} ( X ) \lt \boldsymbol{c}\text{.}\)
    The question of whether the Continuum Hypothesis is true or false is one of the most famous problems in modern mathematics.

    Through the combined work of Kurt Gödel in the 1930s and Paul Cohen in 1963, it has been proved that the Continuum Hypothesis cannot be proved or disproved from the standard axioms of set theory. This means that either the Continuum Hypothesis or its negation can be added to the standard axioms of set theory without creating a contradiction.

Exercises Exercises

1.

Use an appropriate bijection to prove that each of the following sets has cardinality \(\boldsymbol{c}\text{.}\)

(a)

\(( 0, \infty )\)

Answer.

One such bijection is \(f\x ( 0, \infty ) \to \mathbb{R}\) by \(f ( x ) = \ln x\) for all \(x \in ( 0, \infty )\)

(b)

\(( a, \infty )\text{,}\) for any \(a \in \mathbb{R}\)

Answer.

One such bijection is \(g\x ( 0, \infty ) \to ( a, \infty )\) by \(g( x ) = x + a\) for all \(x \in ( 0, \infty )\text{.}\) The function \(g\) is a bijection and so \(\left( 0, \infty \right) \approx \left( a, \infty \right)\text{.}\) Then use Part (a).

(c)

\(\mathbb{R} - \left\{ 0 \right\}\)

(d)

\(\mathbb{R} - \left\{ a \right\}\text{,}\) for any \(a \in \mathbb{R}\)

2.

Is the set of irrational numbers countable or uncountable? Prove that your answer is correct.

Answer.

Use a proof by contradiction. Let \(\mathbb{H}\) be the set of irrational numbers and assume that \(\mathbb{H}\) is countable. Then \(\mathbb{R} = \mathbb{Q} \cup \mathbb{H}\) and \(\mathbb{Q}\) and \(\mathbb{H}\) are disjoint. Use Theorem 9.20, to obtain a contradiction.

3.

Prove that if \(A\) is uncountable and \(A \subseteq B\text{,}\) then \(B\) is uncountable.

Answer.

By Corollary 9.23, every subset of a countable set is countable. So if \(B\) is countable, then \(A\) is countable.

4.

Do two uncountable sets always have the same cardinality? Justify your conclusion.

Answer.

By Cantor's Theorem (Theorem 9.32), \(\mathbb{R}\) and \(\mathcal{P} \left( \mathbb{R} \right)\) do not have the same cardinality.

5.

Let \(C\) be the set of all infinite sequences, each of whose entries is the digit 0 or the digit 1. For example,

\begin{align*} \left( 1, 0, 1, 0, 1, 0, 1, 0, \ldots \right) \amp \in C;\\ \left( 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, \ldots \right) \amp \in C;\\ \left( 2, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, \ldots \right) \amp \notin C\text{.} \end{align*}

Is the set \(C\) a countable set or an uncountable set? Justify your conclusion.

6.

The goal of this exercise is to use the Cantor-Schröder-Bernstein Theorem to prove that the cardinality of the closed interval \([ 0, 1 ]\) is \(\boldsymbol{c}\text{.}\)

(a)

Find an injection \(f\x ( 0, 1 ) \to [ 0, 1 ]\text{.}\)

(b)

Find an injection \(h\x [ 0, 1 ] \to ( -1, 2 )\text{.}\)

(c)

Use the fact that \(( -1, 2 ) \approx ( 0, 1 )\) to prove that there exists an injection \(g\x [ 0, 1 ] \to ( 0, 1 )\text{.}\) (It is only necessary to prove that the injection \(g\) exists. It is not necessary to determine a specific formula for \(g ( x )\text{.}\))

Instead of doing Task 6.b as stated, another approach is to find an injection \(k \x [0, 1] \to (0, 1)\text{.}\) Then, it is possible to skip Task 6.c and go directly to Task 6.d.

(d)

Use the Cantor-Schröder-Bernstein Theorem to conclude that \([ 0, 1 ] \approx ( 0, 1 )\) and hence that the cardinality of \([ 0, 1 ]\) is \(\boldsymbol{c}\text{.}\)

7.

In Exercise 6, we proved that the closed interval \([ 0, 1 ]\) is uncountable and has cardinality \(\boldsymbol{c}\text{.}\) Now let \(a, b \in \mathbb{R}\) with \(a \lt b\text{.}\) Prove that \([ a, b ] \approx [ 0, 1 ]\) and hence that \([ a, b ]\) is uncountable and has cardinality \(\boldsymbol{c}\text{.}\)

8.

Is the set of all finite subsets of \(\N\) countable or uncountable? Let \(F\) be the set of all finite subsets of \(\N\text{.}\) Determine the cardinality of the set \(F\text{.}\) Consider defining a function \(f:F \to \N\) that produces the following.

  • If \(A = \{1, 2, 6 \}\text{,}\) then \(f(A) = 2^1 3^2 5^6\text{.}\)

  • If \(B = \{3, 6 \}\text{,}\) then \(f(B) = 2^3 3^6\text{.}\)

  • If \(C = \left\{ m_1, m_2, m_3, m_4 \right\}\) with \(m_1 \lt m_2 \lt m_3 \lt m_4\text{,}\) then \(f(C) = 2^{m_1} 3^{m_2} 5^{m_3} 7^{m_4}\text{.}\)

It might be helpful to use the Fundamental Theorem of Arithmetic and to denote the set of all primes as \(P = \left\{ p_1, p_2, p_3, p_4, \ldots \right\}\) with \(p_1 \lt p_2 \lt p_3 \lt p_4 \cdots\text{.}\) Using the sets \(A\text{,}\) \(B\text{,}\) and \(C\) defined above, we would then write

\begin{equation*} f(A) = p_1^1 p_2^2 p_3^6, f(B) = p_1^3 p_2^6, \text{ and } f(C) = p_1^{m_1} p_2^{m_2} p_3^{m_3} p_4^{m_4}\text{.} \end{equation*}

9.

In Exercise 2, we showed that the set of irrational numbers is uncountable. However, we still do not know the cardinality of the set of irrational numbers. Notice that we can use \(\Q^c\) to stand for the set of irrational numbers.

(a)

Construct a function \(f\x \Q^c \to \R\) that is an injection.

(b)

We know that any real number \(a\) can be represented in decimal form as follows:

\begin{equation*} a = A.a_1 a_2 a_3 a_4 \cdots a_n \cdots\text{,} \end{equation*}

where \(A\) is an integer and the decimal part \(( 0.a_1 a_2 a_3 a_4 \cdots )\) is in normalized form. (See Exercise 2.) We also know that the real number \(a\) is an irrational number if and only \(a\) has an infinite non-repeating decimal expansion. We now associate with \(a\) the real number

\begin{equation} A.a_1 0 a_2 1 1 a_3 0 0 0 a_4 1 1 1 1 a_5 0 0 0 0 0 a_6 1 1 1 1 1 1 \cdots\text{.}\tag{82} \end{equation}

Notice that to construct the real number in equation (82), we started with the decimal expansion of \(a\text{,}\) inserted a 0 to the right of the first digit after the decimal point, inserted two 1's to the right of the second digit to the right of the decimal point, inserted three 0's to the right of the third digit to the right of the decimal point, and so on.

Explain why the real number in equation (82) is an irrational number.

(c)

Use these ideas to construct a function \(g\x \R \to \Q^c\) that is an injection.

(d)

What can we now conclude by using the Cantor-Schröder-Bernstein Theorem?

10.

Let \(J\) be the unit open interval. That is, \(J = \left\{ x \in \R \mid 0 \lt x \lt 1 \right\}\) and let \(S = \left\{ (x, y) \in \R \times \R \mid 0 \lt x \lt 1 \text{ and } 0 \lt y \lt 1 \right\}\text{.}\) We call \(S\) the unit open square. We will now define a function \(f\) from \(S\) to \(J\text{.}\) Let \((a, b) \in S\) and write the decimal expansions of \(a\) and \(b\) in normalized form as

\begin{align*} a \amp = 0.a_1 a_2 a_3 a_4 \cdots a_n \cdots\\ b \amp = 0.b_1 b_2 b_3 b_4 \cdots b_n \cdots \text{.} \end{align*}

We then define \(f(a, b) = 0.a_1 b_1 a_2 b_2 a_3 b_3 a_4 b_4 \cdots a_n b_n \cdots\text{.}\)

(a)

Determine the values of \(f ( 0.3, 0.625 )\text{,}\) \(f \!\left( \dfrac{1}{3}, \dfrac{1}{4} \right)\text{,}\) and \(f \!\left( \dfrac{1}{6}, \dfrac{5}{6} \right)\text{.}\)

(b)

If possible, find \((x, y) \in S\) such that \(f ( x, y ) = 0.2345\text{.}\)

(c)

If possible, find \((x, y) \in S\) such that \(f ( x, y ) = \dfrac{1}{3}\text{.}\)

(d)

If possible, find \((x, y) \in S\) such that \(f ( x, y ) = \dfrac{1}{2}\text{.}\)

(e)

Explain why the function \(f\x S \to J\) is an injection but is not a surjection.

(f)

Use the Cantor-Schröder-Bernstein Theorem to prove that the cardinality of the unit open square \(S\) is equal to \(\boldsymbol{c}\text{.}\) If this result seems surprising, you are in good company. In a letter written in 1877 to the mathematician Richard Dedekind describing this result that he had discovered, Georg Cantor wrote, “I see it but I do not believe it.”

Activity 52. The Closed Interval \(\boldsymbol{ [ 0, 1 ]}\).

In Exercise 6, the Cantor-Schröder-Bernstein Theorem was used to prove that the closed interval \([0, 1]\) has cardinality \(\boldsymbol{c}\text{.}\) This may seem a bit unsatisfactory since we have not proved the Cantor-Schröder-Bernstein Theorem. In this activity, we will prove that \(\text{ card} \!\left( [ 0, 1 ] \right) = \boldsymbol{c}\) by using appropriate bijections.

(a)

Let \(f\x [ 0, 1 ] \to [ 0, 1 )\) by

\begin{equation*} f ( x ) = \begin{cases}\dfrac{1}{n+1} \amp \text{if \(x=\dfrac{1}{n}\) for some \(n \in \mathbb{N}\)} \\ x \amp \text{ otherwise } . \end{cases} \end{equation*}
(i)

Determine \(f ( 0 )\text{,}\) \(f ( 1 )\text{,}\) \(f \!\left( \dfrac{1}{2} \right)\text{,}\) \(f \!\left( \dfrac{1}{3} \right)\text{,}\) \(f \!\left( \dfrac{1}{4} \right)\text{,}\) and \(f \!\left( \dfrac{1}{5} \right)\text{.}\)

(ii)

Sketch a graph of the function \(f\text{.}\)

Hint.

Start with the graph of \(y = x\) for \(0 \leq x \leq 1\text{.}\) Remove the point \(( 1, 1 )\) and replace it with the point \(\!\left( 1, \dfrac{1}{2} \right)\text{.}\) Next, remove the point \(\!\left( \dfrac{1}{2}, \dfrac{1}{2} \right)\) and replace it with the point \(\!\left( \dfrac{1}{2}, \dfrac{1}{3} \right)\text{.}\) Continue this process of removing points on the graph of \(y = x\) and replacing them with the points determined from the information in Task 52.a.i. Stop after repeating this four or five times so that pattern of this process becomes apparent.

(iii)

Explain why the function \(f\) is a bijection.

(iv)

Prove that \([ 0, 1 ] \approx [ 0, 1 )\text{.}\)

(b)

Let \(g\x [ 0, 1 ) \to ( 0, 1 )\) by

\begin{equation*} g ( x ) = \begin{cases}\dfrac{1}{2} \amp \text{ if \(x=0\) } \\ \dfrac{1}{n+1} \amp \text{if \(x=\dfrac{1}{n}\) for some \(n \in \mathbb{N}\)} \\ x \amp \text{ otherwise } . \end{cases} \end{equation*}
(i)

Follow the procedure suggested in Task 52.a to sketch a graph of \(g\text{.}\)

(ii)

Explain why the function \(g\) is a bijection.

(iii)

Prove that \([ 0, 1 ) \approx ( 0, 1 )\text{.}\)

(c)

Prove that \([ 0, 1 ]\) and \([ 0, 1 )\) are both uncountable and have cardinality \(\boldsymbol{c}\text{.}\)